関数電卓の使い方（座標計算／カシオ）【土地家屋調査士の独学書式講座】

　土地家屋調査士試験では、関数電卓の持ち込みが認められていますので、書式問題（記述式問題）を解くためには、電卓を有効活用して座標計算や面積計算をする必要があります。

　このページでは、土地家屋調査士の書式問題を解くために必要となる関数電卓（カシオ fx-JP500）の使い方について解説します。

※　複素数計算は使用しません。ノーマルな計算方法で解説しますので、ご了承ください。

• 複素数計算については、アガルートの『［中山式］複素数計算』がおすすめです。

おすすめの関数電卓

　まずは、当ページで使用する関数電卓と、おすすめの電卓について紹介します。

カシオ fx-JP500（当ページで使用する電卓）※2023年に生産終了

　土地家屋調査士試験のおすすめの関数電卓は、カシオのfx-JP500という機種です。

　fx-JP500は、それまでのfx-991シリーズとは一線を画す新型電卓として、東京法経学院やLEC、アガルートもすべて、カシオの「fx-JP500」の使用が推奨されるようになりました。

　なお、fx-JP900という上位機種もありますが、土地家屋調査士試験では、JP500で十分です。

カシオ 関数電卓 fx-JP500 （高精細・日本語表示 関数・機能500以上） サイズ： 16.7 x 8.2 x 1.8 cm 参考価格： 3,168円

新おすすめ電卓　Canon F-789SG

　現在（2024年以降）、各予備校で使用が推奨されるようになった電卓が、CanonのF-789SGです。

　カシオのfx-JP500に比べると操作性はやや劣りますが、カシオの後継機種fx-JP500CWに比べると使い勝手は良く、fx-JP500に近い操作が可能とされています。

Canon 関数電卓 F-789SG サイズ： 8.0 x 16.8 x 1.3cm 参考価格： 2,509円

関数電卓の使い方（座標計算／カシオ）

　それでは、実際に事例を使って、座標計算のためのカシオ関数電卓（fx-JP500）の使い方を解説していきます。

　最初に、fx-JP500では、初期設定が分数表示になっているため、

とたたいて、少数表示に切り替えておいてください。

　なお、下記の解説で、メモリーを呼び出す場合に（例えば、を呼び出す場合）
　　　とたたくのと、　　とたたくのは同じです。

　 とたたくと、記憶されているメモリーの一覧から選択する形になりますが、どのキーに記憶されているか確信がある場合は、　　と叩いた方が打鍵数が少なくなります。

座標計算の事例

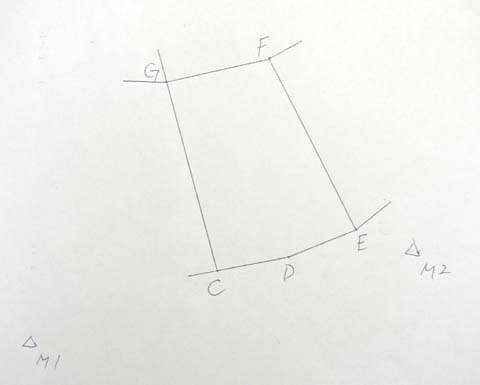
「土地」に関しては、下記の座標値を使用します。（H19 本試験問題）

筆界	Ｘ座標	Ｙ座標
Ｆ	218.55	215.11
Ｅ	207.51	220.79
Ｄ	205.68	216.45
Ｃ	204.73	211.98
Ｇ	216.88	208.43

Ｍ1	200.00	200.00
Ｍ2	206.10	224.47

※ 上記の筆界の並びが、ＦＥＤＣＧとなっていて、ＣＤＥＦＧとなっていないことについては、下記の（3）をご参照ください。

（1） 2点の座標値から距離と方向角を求める

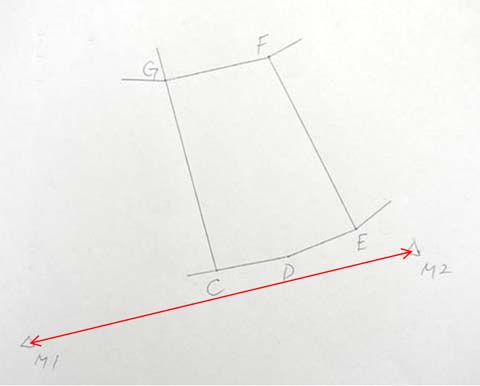
　まずは、M1点とM2点の座標値が与えられた場合に、その2点間の距離と方向角を求める方法です。 

M1（200.00 , 200.00）　M2（206.10 , 224.47）

206.10    200.00  　  224.47    200.00

と電卓をたたくと、
「r＝25.21886001」 ← M1点、M2点間の距離
「θ＝76.00232841」 ← M1点、M2点間の方向角
という値が出ます。

 ※ この時点で、メモリーに2点間の距離、メモリーに2点間の方向角が記憶されています。 

　次に、メモリーに記憶されている数値を呼び出すため、 

とたたくと、「76.00232841」という値が出てくるので、これを60進数（度分秒）の表示に切り換えるため、

とたたくと、「76°0°8.38」となります。 ← M1点からM2点への方向角

（2） 2点間の距離と方向角から座標値を求める

　次は、M1点の座標値は与えられているけれど、B点の座標値が与えられていない場合で、M1点からB点への距離と方向角が与えられているときの、B点の座標値の求め方です。 

M1（200.00 , 200.00）　B（　　　,　　　） 

距離 11.21ｍ　方向角 67°0′8″

11.21  　  67    0    8

とたたくと、
「x＝4.379695729」 ← M1点からB点へのX座標の増分 
「y＝10.310902928」 ← M1点からB点へのY座標の増分
となります。

※ この時点で、メモリーにX座標の増分(⊿X)、メモリーにY座標の増分(⊿Y)が記憶されています。

　次に、M1点のX座標に、B点までの増分(⊿X)を加えるため、 

200.00

とたたくと、「204.3796957」となるので、四捨五入して 「204.38」 ← B点のX座標 

　次に、メモリーに記憶されている数値を呼び出すため、 

とたたくと、「10.31902928」という値が出ます。 ← M1点からB点へのY座標の増分

　そして、M1点のY座標に、B点までの増分(⊿Y)を加えるため、 

200.00

とたたくと、「210.3190293」となるので、四捨五入して 「210.32」 ← 点BのY座標 

（3） 座標値から地積を求める

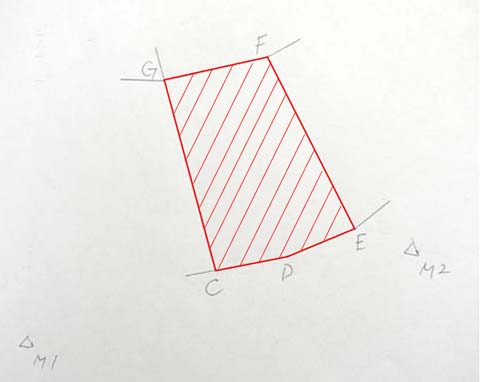
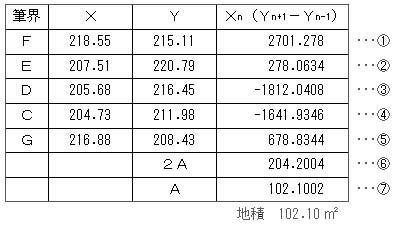
　次は、多角形ＦＥＤＣＧ の各点の座標値が求められた場合の、地積の計算方法です。

筆界	Ｘ座標	Ｙ座標
Ｆ	218.55	215.11
Ｅ	207.51	220.79
Ｄ	205.68	216.45
Ｃ	204.73	211.98
Ｇ	216.88	208.43

　ここで、筆界の並びが、ＦＥＤＣＧとなっていて、ＣＤＥＦＧとなっていないのは、面積を計算するときの計算方法の違いによって、計算結果がマイナス表示となるか、プラス表示となるかの違いが出てくるためです。

　私の計算方法では、多角形の筆界を、時計回りに記載していくと、計算結果がプラス表示となるため、このようにしています。

　下表の一番右の欄の値を、上から順に算出していきます。

218.55　 　220.79　　208.43

とたたくと、「2701.278」と表示され、独立メモリーに記憶されます。　←下表①の数値

以下、同様にたたいていくと、独立メモリーに加算されていきます。

207.51　 　216.45　　215.11

とたたくと、「278.0634」　←下表②の数値

205.68　 　211.98　　220.79

とたたくと、「-1812.0408」　←下表③の数値

204.73　 　208.43　　216.45

とたたくと、「-1641.9346」　←下表④の数値

216.88　 　215.11　　211.98

とたたくと、「678.8344」　←下表⑤の数値

ここまでで、メモリーへの加算は終わりましたので、加算の結果を呼び出します。

とたたくと、「204.2004」　←下表⑥の数値（2Ａ：倍面積） 

これは倍面積なので、面積を求めるため、

2

とたたくと、「102.1002」　←下表⑦の数値（Ａ：面積） 

これが宅地であれば、地積は102.10㎡となります。 

　

（4） 辺長を求める

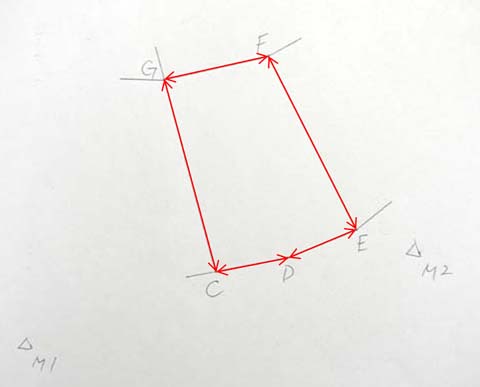
　上述の「（1） 2点の座標値から、距離と方向角を求める。」の計算方法を活用します。 

　まず、計算を始める前に、小数点以下の桁数の設定をします（解答の指示で、「辺長は、小数点以下第3位を四捨五入する」となっている場合）。

これで、計算結果は、小数点以下第3位を四捨五入した値となります。

　まず、ＦＥ間の辺長を求めてみます。Ｆ（218.55 , 215.11)　Ｅ（207.51 , 220.79）
　2点間の距離と方向角を求める要領で、

207.51　　218.55　　　220.79　　215.11

とたたくと、「r＝12.42」という値が出ます。　← ＦＥ間の距離 （少数第3位で四捨五入） 

　次に、ＥＤ間も同様に、Ｅ（207.51 , 220.79）　Ｄ（205.68 , 216.45）

205.68　　207.51　　　216.45　　220.79

とたたくと、「r＝4.71」となります。← ＥＤ間の距離

　この要領で、順に求めていきます。

　なお、小数点以下の桁数を元に戻すには、

とたたくと、元に戻ります。

（5） 2直線の交点を求める

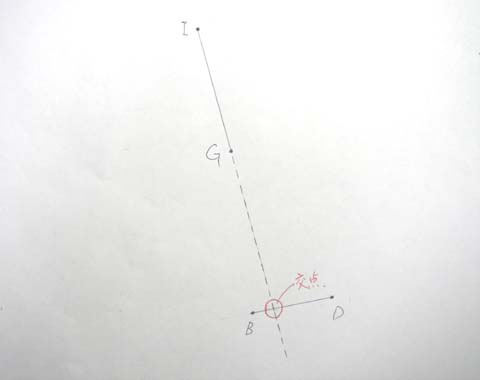
　冒頭の事例の中には書ききれませんでしたが、直線ＩＧと直線ＢＤという2直線があったときの、その交点の座標の求め方です。（この事例では、直線ＩＧの延長線と、直線ＢＤとが交わります。）

Ｉ（226.66 , 205.57）　Ｇ（216.88 , 208.43）
Ｂ（204.38 , 210.32）　Ｄ（205.68 , 216.45）

　直線の方程式は、Ｙ＝ａＸ＋ｂ　と表されます。 この直線の傾き「ａ」は、上述の「（1） 2点の座標値から、距離と方向角を求める。」の計算方法を活用して求めます。

　まず、ＩＧ間の方向角を求めるため、

216.88　　226.66　　　208.43　　205.57

とたたくと、メモリーには2点間の方向角が入っているので、

とたたくと、「-0.292433537」となります。　← 直線ＩＧの傾き「ａ」 

これを、メモリーに記憶させるため、

とたたきます。

　次に、切片「ｂ」を求めるため、式を変形します。 ｂ＝Ｙ－ａＸ
　Ｉ点でもＧ点でもどちらでも構いませんが、例えば、Ｇ点の座標値を代入するとして、

208.43　　　　　216.88

とたたくと、「271.8529857」となります。　← 直線ＩＧの切片「ｂ」 

　これを、メモリーに記憶させるため、

とたたきます。 ここまでで、直線ＩＧの方程式は、Ｙ＝Ｘ＋ となっています。

　次に、直線ＢＤの方程式についても同様に、メモリー と を使って、Ｙ＝Ｘ＋　となるようにします。（メモリーには「4.715384618」、には、「753.4103082」が入ります。）
　この方程式の解は、

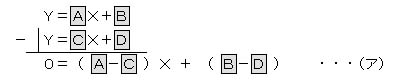
で求められるので、 まず、 － を求めるため、

とたたくと、「-4.715384618」となり、これを、メモリーに記憶させるため、

とたたきます。

　次に、 － も同様にして、メモリーに記憶させます。（「961.8403082」） 

　これで、上記（ア）の式が、0＝Ｘ＋ となったので、式を変形して、Ｘ＝－ / とし、

 とたたくと、「204.7325326」となるので、四捨五入して、「204.73」← 交点のＸ座標 

　これを、Ｙ＝Ｘ＋　の式に代入すれば、 

204.73

 「211.9830675」となり、四捨五入して、「211.98」となります。← 交点のＹ座標

関数電卓の使い方（床面積の求積／カシオ）の解説

　土地の座標計算については以上です。

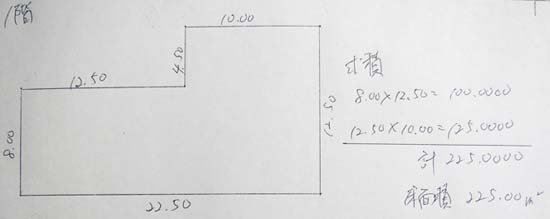
　次は、建物について、カシオ関数電卓の使い方を解説します。

　建物の書式問題を解く際は、土地の座標計算のような特別な電卓操作は求められませんので、床面積を求める方法のみ記載しておきます。

2つの四角形に分けて床面積を求める

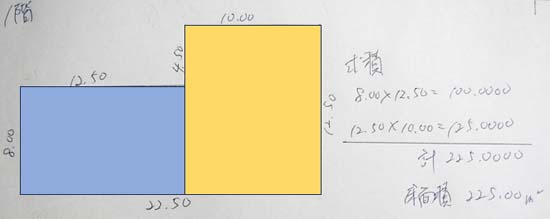
上図のような場合、四角形2つに分けて面積を求めますので、

求積
　12.50×10.00＝
　8.00×12.50＝
として、メモリーに加算しながら、計算をします。

12.50　　10.00

とたたくと、「100」となるので、「100.0000」と書き込み、続いて、

8.00　　12.50

とたたくと、「125」となるので、「125.0000」と書き込みます。そして、メモリーを呼び出すため、

とたたくと、「225」と出るので、計 「225.0000」となります。

　

＜書式対策（独学講座）＞
関数電卓｜地積測量図｜各階平面図｜建物図面